Distributed computing over Internet using a peer to peer network

20 September 2002

The main goal of this open source project work is to design and implement a prototype for an application which shares CPU-time of normal computers connected to the Internet.

To do this, the application connects to a peer to peer network and is able to share files with others. In addition the application, from now on simply called the node (to emphasize the idea that the application is a network’s node) is able to send, receive and perform some computational jobs.

Jobs travel through the peer to peer network disguised as a search string for files. They travel until they find a node willing to execute them or until their short life terminates, limited by a counter decremented every time the job is retransmitted.

Once the good-willing node finishes a job, it returns the result to sender. The sender collects results the same way it does for files found on the network.

Jobs are described in polish notation, which can be interpreted as commands for a stack. "1 + 1" becomes "1,1,+"; although at first look this system seems complicated, it frees the node from some difficult issues like operator precedence and bracket management.

The application implements the commands for the computation in an elegant way, making it easy to extend the set of basic computing functions the node knows about.

A plugin for computing the discrete logarithm in modulo arithmetic over large integers is implemented in the framework as an example for a working extension.

The application and the ideas behind the scenes are documented, so that others can understand how the system works, and eventually write plugins if they are interested. A discussion of the system’s capability, details of its implementation, as well as possibilities for its extensions conclude the report.

Frameworks for distributed computing

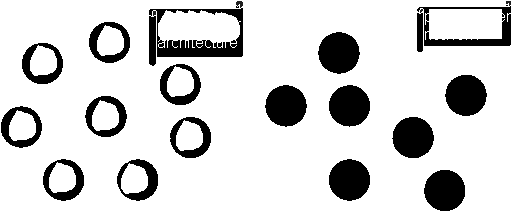
Important distributed computing projects over the Internet, such as Seti@home [6] and the Cancer Research project [7], use a centralized architecture, called "client-server" architecture : one well known server distributes different chunks of data to all clients, while the clients get the data and perform a computation on that data. In the centralized network there is one server, while all other nodes are clients that work for the server. Clients connect only for the necessary time to download the data. They then perform some kind of computation and return the result to sender, usually many hours later.

The network’s shape is a star. The server lies at the star’s center and the rays connect all clients to the server. If the server experiences a problem and goes down, the whole network doesn’t work anymore.

We are interested in a different architecture, a so called "peer to peer network". In a peer to peer network (shortly abbreviated with P2P) all nodes are at the same time client and server. There is no privileged node that can claim to be different from others. All nodes can send out data and all have to work if requested by another node.

In addition, the nodes stay online while they perform computations without disconnecting. A thread on the node keeps connections and forwards packets through the network. In the meanwhile, other threads perform computations on chunks of data and return them to their initiator. Different algorithms can be stored in plugins that extend the functionality of the node.

In the P2P model the topology is not limited to a star, the network can assume any possible connected shape.

As you can see, the centralized model is a subset of the peer to peer model. Using a peer to peer network it is still possible to perform a centralized computation.

Two practical advantages of the P2P model are its "lack of a single point of failure", as stated in [9] and the fact that P2P doesn’t require to configure and design networks. The network designs itself.

The price for that flexibility in P2P is mostly paid by reduced bandwidth; in other words lot of packets are directed often on wrong ways and some of them are just to administrate the irregular network. In an irregular topology nodes connect and disconnect in a chaotic fashion, so that packets can be lost.

The author believes that with the current technological developments, moving hardware towards higher bandwidth and cheaper 24-hours connections (ADSL), and software with simple and powerful improvements to the P2P model (like "random walkers" that could reduce traffic of two orders of magnitude [1]), we will see the P2P model applied to distributed computing.

What is the Gnutella Network ?

In this chapter we explain how the Gnutella network works by showing an application implemented using a Delphi [14,15] component (written by Cap’n Bry [11])

The Gnutella network is a peer to peer network built on top of the TCP / IP protocol with the goal of sharing files of any type. Nodes willing to connect, randomly pick up other nodes from a list, which is delivered by a special node called host catcher. Once the node has established some connections to other online nodes (four or five), it tries to stay connected as long as possible: it will attempt to replace connections, if the established ones break down. Over the connections the nodes exchange packets.

Packets contain search strings for files and information for establishing connections correctly. In this project, to these packets we also add commands for computations. Here, a packet carrying these commands is called job.

The three principles of Gnutella :

1. The network has no privileged nodes, there is no fixed clients nor fixed server. Every node in the network is server and client at the same time. This means every node is able to use services from other nodes and has to offer services to other nodes.

   
   



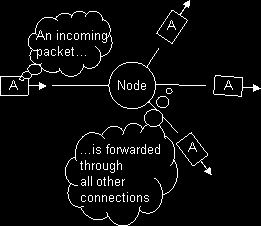
2. Packets are routed through the network with the simplest mechanism possible. Once a packet reaches a node it is immediately sent out over all its other connections. This mechanism of routing packets is called ‘flooding’. The only guarantee the network mechanism provides, is that a packet sent out from a node will reach every other node connected to the sender node.




3. To prevent the geometric growth of duplicated packets, two mechanisms are defined. First, a packet carries a counter which is decremented every time the packet is forwarded again. Once the counter becomes zero, the packet will be deleted. This counter is called TTL (Time To Live) and prevents packets from travelling indefinitely. A consequence of the counter is that a packet will only reach nodes in the so-called TTL-radius.

   The second mechanism is the following: every host keeps a list of packets the host saw in the last minutes. Every packet coming in will be checked with the list. If the packet is already present, the new copy is thrown away. If not present, the packet is added to the list and resent using the flooding mechanism. This will prevent packets from travelling in circles. The measure wouldn’t be necessary in loop-free topologies (trees), because there packets cannot replicate themselves. Of course, the Gnutella network is a complex graph with a lot of loops.

   The list is also used to route back answers to queries. Answers follow the shortest path in the network and are not routed using a flooding mechanism

Details of the protocol are defined in [3]. History of Gnutella can be read in [5]. In [4] there is strong criticism to the scalability of Gnutella from one of Napster’s [10] authors.

A further improvement to the Gnutella protocol is presented here and was implemented in our application. The improvement reduces the necessary bandwidth for the peer to peer network.

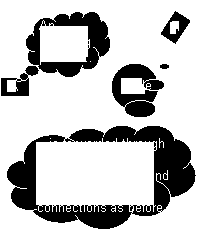
The picture above illustrates the necessary change in the routing mechanism to implement "random walkers". Compare this picture with the previous one. In the previous picture, the incoming packet is forwarded to all connections, except the one where the packet came in. In the random walkers mechanism, we simply choose one connection at random (notice that the connection could be the incoming connection, too). Now one packet doesn’t multiply itself every time it is forwarded. The packet simply randomly "walks" over the peer to peer network, like a drunk on a hard night. The drunk doesn’t clone itself at every crossroad of the city, and this is a good news for the network bandwidth. Intituitively a sent packet doesn’t produce a flood of packets that grow geometrically, but stays alone and alive until its Time To Live counter becomes 0.

The question is now how many walkers are necessary to reach a sufficient number of network’s nodes, so that our network’s queries (e.g search for files or computational requests) return enough results?

In "Search and Replication in Unstructured Peer-to-Peer Networks" [1] ([9] for a review), a joint team at the Universities of California at Berkeley and Princeton propose showed through computer simulation that to begin a network query, a number between 16 and 64 random walkers are enough and suitable. However, the random walkers should check back with the requester before walking to the next node (note that checking is not implemented yet in the presented framework).

The process involving random walkers can be observed in real life. Physicians often name it diffusion. The diffusion process can be described by a partial differential equation (called heat equation) and the solution is a bell curve that shows how the density of random walkers decreases from the central point, where the diffusion process started [8].

Description of the virtual machine inside the node

Our application effects a virtual machine for interpreting computational commands. Once a command is typed and the ‘Compute locally’ button is clicked or once an incoming job is caught from network, the virtual machine interprets it. (See the screenshots section to get an idea)

As an example, let us look at the simple "1,3,add" command. The virtual machine reads arguments each separated by a comma. If the argument is a number (like "1" and "3"), it is loaded on the stack. If the argument is a command (like "add"), the virtual machine searches in all dynamic link libraries in the directory plugins for a method called “add”. Then the virtual machine calls that function, the argumets for the functions are popped and the result is pushed onto the stack. Normally most of the functions just crunch some parameters and give one parameter back. Look at another more complicated example:
Example: 3,1,add,7,mul
Here is the behaviour of the virtual machine, step by step :

1. Stack : empty
   String : 3,1,add,7,mul
    
2. Stack : 3
   String : 1,add,7,mul
   Here the number 3 is loaded on the stack
    
3. Stack : 3,1
   String : add,7,mul
   One is loaded on the stack, too
    
4. Stack : 4
   String : 7,mul
   The command add first pops the two parameters from the stack. Then it computes 3+1, the sum of the two parameters. The result, 4, is pushed on the stack
    
5. Stack : 4,7
   String : mul
   7 is pushed on stack
    
6. Stack : 28
   String : empty
   4 and 7 are pooped. The final multiplication is computed and the result 28 is pushed. The empty string signalises that we are finished.
    

Computation using interpreted strings is slow way. In fact the virtual machine is about 500 times slower than compiled code. Why 500 times? Because about 500 assembler commands are used to find out where the function with that command name lies in the plugins. The virtual machine is more intended for small adjustments to the parameters. Big tasks should be done by plugins that implement the whole algorithm. These algorithms are compiled in the dynamic link library. They run maximum speed, the speed of machine compiled code.

A nice example is the following :
compare the speed of :
"0,{rnd,sqr,rnd,sqr,add,1,less,add},1000000,rpt,1000000,dvd,4,mul"
with the speed of
"100000000,pi"

Both commands do the same: they compute pi using the Monte Carlo method (described in Appendix A). However, the first one leaves the whole computation to the virtual machine, while the second one only uses the virtual machine to find the appropriate compiled code among the plugins (in this case, the source code for the function pi is in greekpi.dll).

On a 1GHz Pentium III the first command takes about 40 seconds. The second command takes about 8 seconds. However the second command uses a sample of 100’000’000 while the first only one million. So, 40 seconds for 1’000’000 throws and 8 second for 100 millions throws shows that if we rely on the virtual machine, we are 500 times slower.

Earlier versions of the application presented here were only 20 times slower when using the virtual machine before the plugin mechanism was implemented.

Another limit of the virtual machine can be seen from the example : the virtual machine has a sample limit of 1’000’000 because the command "rpt" recursively calls the procedure used in its computation; every time a sample datum is executed more space is reserved in memory. Once the memory stack is full, Out of Memory errors occur.

Implementing a new plugin in the application framework

As stated in the previous section, the virtual machine is not suitable for fast computations. However our application offers a framework where plugins can be installed. The plugins are compiled code; so there are no performance losses caused by the virtual machine, except the initial overhead to search for requested functions among the plugins.

Physically, plugins are dynamic link libraries in the subdirectory /plugins of the application. They are loaded when the application is created.

Dynamic link libraries are a collection of procedures and functions (methods in C-terminology). So a plugin, as a collection of functions, can implement more than one command which can be directly typed in as commands in the "Computing" page of the GPU window (GPU [13] is the name for our application, see Appendix D for some screenshots); e.g the plugin basic.dll exports the functions add, mul, sqrt and many more...

The source code of a plugin is split in two files. One is a main file specifying which functions have to be exported (only these functions can be used from the main application GPU, all others stay hidden). The other file contains the source code of the functions.

As example of the main file, here the main file basic.dpr, which is part of the plugin basic.dll :

As we said, the main file specifies the functions to be exported. The file where the source code of these functions is defined is specified in the "uses" clause. In the example the file for the plugin basic is called basicdll, and is found in the same directory of basic.dpr with name basicdll.pas
Now take a closer look at the file basicdll.pas :

Between the keywords interface and implementation, we define the signature of the functions. To avoid nasty runtime errors, it is important that exported functions use this signature :

The function name in this case is "tobeexported". A strange parameter of the type Tstack is passed to the function (this is explained below) and the function result is a boolean type (true or false). By definition, a function returns true if the computation could be done without any problems, and false is something went wrong: for example if the parameter Tstack was incorrect.

The keyword "stdcall;" means the function is a "standard call" and informs Delphi [14,15] that the function is a function in a library, which will be loaded at runtime. For these functions the address cannot be known a priori in the linking process.

Here are some important things about the strange parameter of type Tstack :
Parameters are passed to the function with a record of type Tstack (a record is a struct in C-terminology). The record fields of TStack are defined in the file commonconst.pas. Here the record definition, as it is in commonconst.pas :

The field Stack is an array of floating point numbers, with size MAXSTACK, which is a constant defined in commonconst.pas.
The field StIdx is actual index in the array Stack, and can be viewed as an array pointer.

Imagine now that someone calls the function add, using the GPU command
3,7,add.

The main GPU application will first create and fill a record of type Tstack like this :

Parameters, record of type Tstack, containing the following :
    Stack = [3,7, not defined, not defined, not defined, not defined, ...]
    StIdx = 2

Note that the StIdx points always to the last defined value in the array and that arrays in Delphi begin with index 1 and not 0, unlike C.
GPU will search in all plugins in the /plugins directory for a function called add. GPU will find it in the dynamic link library basic.dll. GPU will call add and pass the record Parameters by reference (in Delphi values passed by reference are marked by the keyword var). By reference (or "call by address") means that the function works with the same record as the main application, changes are visible for both. This is the opposite behaviour to "call by value": there the function works with a copy of the record, and changes will be lost when the function returns.

Conclusion

Our hope is that people interested in science will run an application like the one presented here. The difference between this framework and frameworks with centralized distributed computing (like the Seti@home project is [6]) is that anyone can send out jobs and develop extensions for the application. At the beginning, people should learn confidence with the machine by sending out simple jobs. Other machines will respond and the psychological impact could be the following: people running the application aren’t only part of a project for a supercomputer, they can control the supercomputer, too. Developing extensions for applications like this could become an exciting sport, perhaps as exciting as virus development is but with more positive consequences.

The application source code and the executables [13] can be downloaded from the Internet address http://sourceforge.net/projects/gpu. The project is now published as Open Source and a team of people of different nationalities is looking forward to improve the code, as well as documentation.

APPENDIX A

Greekpi is a plugin which computes Pi with the Monte Carlo method. Although not very useful in real life (206 billion of digits of Pi are known [12]), it is a good academic example. The idea is to generate two random numbers between 0 and 1, which are considered as coordinates in the plane. Let’s call these two coordinates x and y. Now the plugin checks if the point (x,y) lies within a circle of radius 1. To do this square x and y, sum them together and check if the result is less than one.

If the point (x,y) lies in the circle, increment the counter Sum by one.
By repeating this operation many times, if the points are uniformly distributed, we can build the quotient between the counter Sum and the number of throws (in the plugin the number of throws is passed as parameter and stored in the variable) and we get the percentage of throws falling within the upper right quadrant of the unit circle. Recall that the points can only be thrown between the square with side 1 and area 1. The percentage becomes also the area of the quarter of the circle with radius 1. By multiplying the percentage by 4 we get the complete area of the circle, which is Pi.

Here the source code for the plugin Pi.

function pi(var stk : TStack):Boolean;stdcall;
 var
    Idx         : Integer;
    Count,Sum,i : Longint;
 
 begin
 Result := False;
 Idx := stk.StIdx; {this should speed up and also made the code more readable}
 {check if enough parameters
  first parameter is number of throws for computing Pi}
 if Idx < 1 then Exit;
 Count := Trunc(Stk.Stack[Idx]);
 if Count > 625000000 then Exit; {parameter is too big and we get an overflow}
 
 Sum   := 0;
 for i:=1 to Count do
           begin
            if (Sqr(Random)+Sqr(Random)) < 1 then
                Inc(Sum);
           end;
 
 {gives result back}
 Stk.Stack[Idx]:=4* Sum / Count;
 Result := True;
 end;

APPENDIX B

One-way functions are functions that are very easy to compute in one direction, but very difficult to invert. One of the simplest functions with that one-way property is the power modulo a number.
2 to the power of 5 is 32. Modulo is the simple operation that gives the remainder of a division between two numbers, e.g. 32 modulo 19 is 13.
2 to the power of 5 modulo 19 is 13.
2^5 mod 19 = 13

Easy way round

There are two ways offered by GPU to compute the power modulo a number.
Switch to the Computing page and type ‘2,5,19,powmod’, then click on ‘Compute locally’ and see if the result matches. ‘powmod’ is implemented in this way: a loop multiplying 2 for 5 times with itself; each time the modulo operation is performed. The source code of ‘powmod’ can be found in basicdll.pas.

It turns out that there is a more efficient way to compute this special power. It uses the property that (2^3)^4 = 2^(3*4) = 2^12 . The previous plugin used n multiplications, if it were computing 2^n mod x. The plugin implemented in cryptodll.pas uses an algorithm called ‘Square and multiply’. For the same task with n as power, only about logarithm with base 2 of n loops are needed. Try the following task ‘2,5,19,squareandmul’ in GPU. Refer to cryptodll.pas to see how the Square and Multiply algorithm works in detail.

To compare the two plugins, measure how long it takes '11,60000000,5999,squareandmul' compared to '11,60000000,5999,powmod'.

Another weakness of ‘powmod’, is that it can’t handle big numbers. Big jobs may result in different results, especially if you choosed a modulo that is higher than 32 bits.

Now let’s take it the other way round. If someone asks you the following: how many times should I multiply 2 if I want to get 13 modulo 19? Ok, you know from the previous example, that the right answer is 5.

If you forgot it, you could just try to build a table and see where the number 13 comes up in the right column. But, good look if the modulus is 70383776563201.

For a computer, the approach of building such a table is too expensive in time and memory space. Here the one-way property shows itself clearly.

For this reason, GPU implements an algorithm that tries to solve the problem using the baby step / giant step algorithm. This algorithm uses only a table with a size of the square root of n, where n is the modulus. For further information, refer to the source code in the plugin cryptodll.pas. The function name is ‘discretelog’.

Let us ask GPU to perform the computation: this is the packet sent out and it has a lot of parameters, explained later. Type ‘13,2,19,4,0,discretelog’. Again, click on the ‘Compute locally’ and see if the result is 5. The result 5 is called the discrete logarithm of 13.

You encountered the first three parameters above (’13,2,19’). In cryptography 13 is the most important parameter. Normally the other parameters are given from cryptographic algorithms, and what we search for is only the discrete logarithm. 2 is sometimes called the generator of the cyclic group, or in other texts, the primitive root, because it generates the integers between 1 and 18, if we exponentiate 2 with numbers between 1 and 18 modulo 19. Note that if we compute 2^19 mod 19, we get again 2, which is the same as we compute 2^1. This is the reason why this particular mathematical structure is called cyclic group.

Elements of the group are the ones between 1 and 18, and the order they come in the structure is given by the operation 2^x mod 19 performed over the numbers between 1 and 18.

Better said, the result 5 is the discrete logarithm of 13 with primitive root 2 over the cyclic group with modulo 19 and multiplication as operator.

The order of the group is 18, because there are 18 different elements that can be generated. Please note in decyphering that it is difficult to choose a primitive root, and size of the group in order to get them to generate a whole group. There are some constraints for the modulo operator (19). The modulo number has to be relative prime to all other elements in the group. E.g if you choose 2 as primitive root, and 16 as modulo operator, you won’t get all numbers between 1 and 15 to be generated. The table here explains the situation :

This desaster happens because 16 and the group element 4 have the factor 2 in common. In conclusion, the modulus p has to be prime, in order to generate all numbers between 1 and p-1.

Before starting the big computation the last two parameters in ‘13,2,19,4,0,discretelog’ need to be explained. The baby step, giant step algorithm uses a system with milestones. Milestones are simply elements of the group (defined in the section “Difficult way round”) in a fixed distance between them.

Now the parameter 4 explains itself: this is the number of milestones the program creates.
The distance between the milestones is chose by the plugin itself; it is the square root of n, where n is the modulus. You shouldn’t specify more than sqrt(n) milestones, or else the sorting algorithm won’t work, because the algorithm generates duplicates and indexes are not powers of the generator anymore. Our plugin checks this, and if the number is too big, it defaults to sqrt(n).

We can now imagine computations where the memory space of one machine is not enough to contain all milestones. In fact, GPU normally doesn’t digest more than one million milestones.

The idea is to choose at random a starting point, in the big circle built by the elements of the group, if they are ordered using the power function. The perimeter of the circle is named with real numbers from 0 to 1. In other words we normalize the element index (that is a number between 1 and the order of the group) to a real number between 0 and 1.

Computing this packet ‘11412647538025,11,70383776563201,1000000,rnd,discretelog’ will take about 10 minutes on a 1GHz machine (August 2002). Here we use one million milestones, although seven million (sqrt(70383776563201)=7 million) are needed to cover the whole circle of the huge cyclic group. So about 70 minutes are needed to solve the task.

Using rnd as parameter we get an easy way to parallelize the Baby step / gian step algorithm. By sending the above packet to a small network of GPUs, they will start to generate from a random starting point a part of the table needed to find out the discrete logarithm. Most of GPUs will respond with a ‘0’ because they didn’t find the discrete logarithm. However, soon or later, a GPU will generate a table that covers the discrete logarithm and will send back the correct result.

APPENDIX C

Imagine having five workstations available, where we can install the presented application, called GPU, an acronym for Global Processing Unit. If you are a student, you can try to reserve some workstations in the computer room. Between semesters many students are in holiday and the computer rooms are mostly empty.

We deactivate on all installed GPU’s the feature “Automatic connection management”, so that the program doesn’t connect automatically to other workstations located somewhere outside the local network. Now using the ‘Add’ button in the Monitor page of the GPUs, you can build a network with the shape you want. E.g. you can build a circle, a star... Notice that a connection is two-way, so you can add a connection from A to B, but later you can’t add one from B to A. Connections are numbered in the way you add them. So in the picture below A-C was added before A –B. The numbering is relative to the node, and corresponds to the order of the established connections list.

In the following example we decide to connect the five workstations as a tree. A tree is an efficient topology, there are no loops where packets can multiply...

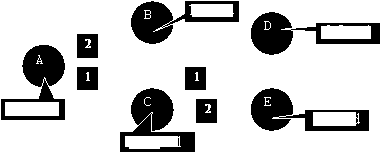
We sit in front of Workstation A, and we want our “complex” computation to be performed from B,C,D and E. D computes 2 times 3, E computes 8 divided by 4, C multiplies the results of D and E together, B computes 1 plus 1, and A finally adds the results from B and C.

If you type in that huge string in the computing page of GPU, you’ll get back the result 14.
As you can see, recursion is required to build up packets. We don’t have in this case a central server that distributes jobs. In conclusion that system of differentiating jobs using recursion is in my eyes pretty useless. The problem comes from the way the virtual machine computes and distributes jobs. To solve the problem, we could think at a virtual machine that distributes tasks numbering nodes and distributing them lists.

References